LaTeX templates and examples — Math
Recent

Funktionsuntersuchung, Übung 1

Las observaciones han mostrado que el numero de neutrinos electrónicos νe que llegan a la tierra desde el sol es aproximadamente la mitad del número esperado de nuestro conocimiento de las reacciones nucleares que ocurren al interior del sol. Estas observaciones se explican como el resultado de que algunos neutrinos electrónicos νe se convierten en neutrinos muónicos νμ y neutrinos tauónicos ντ durante su recorrido entre su creación al interior del sol y su observación en la tierra. Este cambio de un sabor a otro se conoce como oscilaciónes del neutrino. Se introduce un término de masa para el neutrino que es invariante de Lorentz en la densidad lagrangiana del modelo estándar (SM), y se describe el estado del neutrino |να⟩(α = e, μ, τ) como una combinación lineal de autoestados de masa |νi⟩ (i=1,2,3), lo cual conduce a las oscilaciones del neutrino.
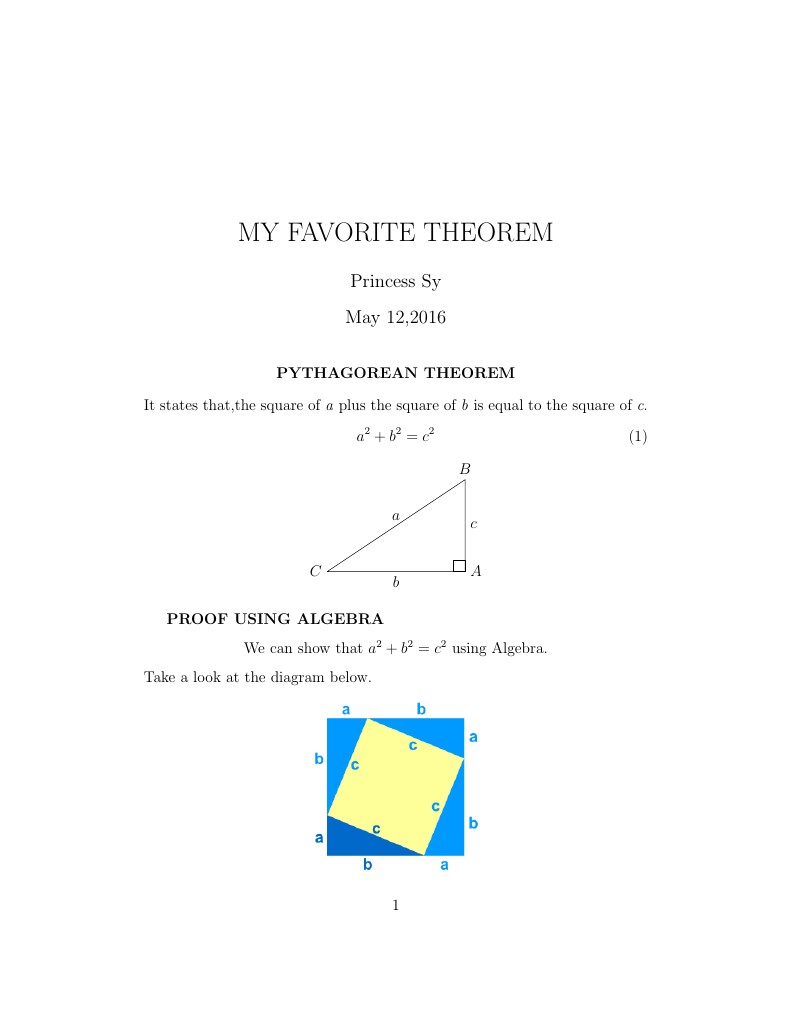
A requirement for our Math330 class.

Übung: Lineare Gleichungssysteme

trabajo realizado para la cátedra de señales y sistemas

Basic homework assignment template.

The output of this table is used as Table 2 of the paper: Wangyan Li, Zidong Wang, Guoliang Wei, Lifeng Ma, Jun Hu, and Derui Ding, “A Survey on Multisensor Fusion and Consensus Filtering for Sensor Networks,” Discrete Dynamics in Nature and Society, vol. 2015, Article ID 683701, 12 pages, 2015. doi:https://www.hindawi.com/journals/ddns/2015/683701/cta/

This is a simple step by step on how to do mathematical induction.

How to derive the Taylor series for the Lambert W function. The Lambert W function is the inverse of the function x ↦ xex.
\begin
Discover why over 25 million people worldwide trust Overleaf with their work.